
ВЗАИМОДЕЙСТВИЕ ЗДАНИЯ И ОСНОВАНИЯ: МЕТОДИКА РАСЧЕТА И ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИ ПРОЕКТИРОВАНИИ
А.Г.Шашкин, К.Г.Шашкин
| Главная страница сайта |
| Титульная страница журнала |
| Содержание тетради |
4. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ СОВМЕСТНОГО РАСЧЕТА ОСНОВАНИЯ И ЗДАНИЯ
Расчет надземных конструкций с использованием численных методов в настоящее время успешно входит в повседневную проектную практику. Конструкции здания моделируются стержневыми и пластинчатыми элементами, в ряде случаев используются трехмерные упругие элементы. Существует большое количество отечественных и зарубежных программ, позволяющих рассматривать конструкции, набранные из такого рода элементов. Некоторые модели содержат и учет нелинейных свойств материалов надземных конструкций.
В программе "FEM models" использованы традиционные подходы к моделированию работы надземных конструкций, ставшие привычными для проектировщиков. Более того, расчетные схемы таких популярных программ как SCAD, ЛИРА могут свободно конвертироваться в среду "FEM models". Это же относится и к чертежам, выполненным в программе AutoCAD.
Принципиальным отличием "FEM models" от традиционно применяемых программ является возможность моделирования основания с использованием широкого спектра моделей работы грунта.
При выборе модели работы грунта следует руководствоваться следующими обстоятельствами:
1. В какой мере деформаций рассматривается работа основания.
Для задач о влиянии на напряженно-деформированное состояние основания дополнительного статического нагружения весом проектируемого здания вполне приемлемым является допущение о малости деформаций по отношению к размерам деформируемой области. Это же допущение остается справедливым и при рассмотрении осадок здания вблизи огражденных котлованов подземных сооружений, естественных откосов, набережных и т.п. Гипотеза о малости деформаций неприемлема лишь при рассмотрении смещений, сопоставимых с размерами деформируемой области (процесс оползания склона, потери устойчивости, стенок или забоя буровой скважины, влияние погружения готовых свай на массив грунта и т.п.). Поскольку в настоящей публикации этот класс задач нами не рассматривается (Рассмотрению больших деформаций массива грунта посвящены работы В.Н.Парамонова (1999, 2000), ниже мы ограничимся лишь малыми деформациями основания.
2. Какое состояние массива грунта рассматривается: стабилизированное или нестабилизированное.
Если расчетчика интересуют конечные осадки здания, можно использовать модели стационарных процессов. К ним относятся модель линейно-деформируемой (квазиупругой) среды, нелинейно-упругие модели, деформационная теория пластичности, теория пластического течения, модели упрочняющихся сред (так называемые шатровые модели), теория упругопластических процессов.
Если же необходимо рассмотреть поведение массива грунта во времени, применяются модели нестационарных процессов: теория фильтрационной консолидации, теория ползучести.
Необходимость учета фактора времени и, соответственно применения моделей нестационарных процессов, возникает в случаях, если
- отсутствует подобие между конечным напряженно-деформированным состоянием основания и расположенного на нем здания и состоянием в процессе деформирования (нагружения);
- здание строится в несколько очередей;
- здание строится в непосредственном примыкании к существующему, осадки которого не стабилизировались (причиной этого может быть развитие длительных процессов деформирования основания, а также внешние техногенные факторы - динамические воздействия от транспорта, гниение лежней, обводнение грунтов техногенными водами, загрязнение грунта и т.д.).
Как показывает опыт, использование моделей стационарных процессов позволяет решить большинство практических задач и выявить при этом основные закономерности деформирования массива грунта и надземных конструкций.
Решение нестационарных задач во многих случаях затруднено отсутствием достоверных параметров поведения грунта во времени и чаще всего требует проведения специальных дополнительных исследований. В дальнейшем основное внимание уделим рассмотрению стационарных процессов.
3. Рассмотрение каких физических процессов, происходящих в грунте, существенно для понимания работы массива грунта и покоящегося на нем здания.
Расчет конструкций и грунтовых оснований выполняется по двум группам предельных состояний. Расчет по первой группе предельных состояний заключается в недопущении потери прочности и устойчивости конструкции или основания. Основой аналитических методов определения несущей способности основания является теория предельного состояния.
В отличие от методов расчета конструкций, нелинейная работа которых, как правило, не допускается, действующие нормы допускают развитие в грунте локальных зон пластических деформаций даже при рассмотрении линейно-упругой работы основания. Соответственно широкое применение в практике геотехнических расчетов получили физически нелинейные модели работы грунта. Среди них наибольшую популярность приобрела теория пластического течения. В этой теории, развитой Прандтлем и Рейсом приращения деформаций рассматриваются как сумма приращений упругой и пластической составляющих:
![]()
Приращения упругих деформаций определяются соотношениями
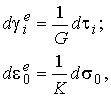
а приращение пластических деформаций
![]()
При этом предполагается, что тензор приращения пластических деформаций пропорционален тензору напряжений:
![]()
где dl - некоторая функция, характеризующая пластическую часть приращения деформаций.
Друкер и Прагер, обобщая теорию пластического течения, ввели понятие потенциала пластичности f, подразумевая под ним такую функцию напряжений, частная производная от которой пропорциональна приращению пластической деформации:
![]()
Отсюда следует, что вектор пластических деформаций перпендикулярен поверхности пластического потенциала.
Основной задачей теории пластического течения является описание поверхности текучести в пространстве напряжений, по достижении которой возникают пластические деформации.
В простейших моделях эта поверхность стационарна и является предельной. В механике грунтов такие поверхности описываются уравнениями фон-Мизеса, Треска, Кулона - Мора. Менее известны поверхности, описываемые зависимостями, предложенными Гениевым:
![]()
|
где K=const;
|
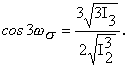 |
Связь между параметрами прочности Гениева и Кулона - Мора имеет вид
![]()
Ломизе предложил следующую зависимость:
![]()
где ti- интенсивность напряжений сдвига; s0 - среднее напряжение; F, N, a - экспериментальные константы.
Если поверхность текучести совпадает с поверхностью пластического потенциала, закон течения называют ассоциированным, в противном случае - неассоциированным. Примером последнего является равнообъемное течение с предельной поверхностью, не параллельной гидростатической оси.
Развитие вычислительной техники способствовало разработке численных методов реализации таких моделей, что позволило выполнять расчеты оснований за пределами расчетного сопротивления с использованием традиционных характеристик, определяемых при инженерно-геологических изысканиях.
Последнее обстоятельство чрезвычайно важно, поскольку применение большинства более сложных и тонких моделей становится попросту невозможным без определения специальных механических параметров при проведении инженерно-геологических изысканий. Таким образом, следует признать, что в настоящее время пятипараметрическая теория пластического течения (параметры: g, Е, n, с,j) находится вне конкуренции среди моделей стационарных процессов по возможности массового использования в практике проектных расчетов.
| Ответы специалистов | Новости геотехники | Интернет-журнал |
| Семинары и конференции | Компьютерные программы | Полезные ссылки |