ВЗАИМОДЕЙСТВИЕ ЗДАНИЯ И ОСНОВАНИЯ: МЕТОДИКА РАСЧЕТА И ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИ ПРОЕКТИРОВАНИИ
А.Г.Шашкин, К.Г.Шашкин
| Главная страница сайта |
| Титульная страница журнала |
| Содержание тетради |
1. ИСПОЛЬЗОВАНИЕ УПРОЩЕННЫХ МОДЕЛЕЙ ОСНОВАНИЯ ДЛЯ РЕШЕНИЯ ЗАДАЧ СОВМЕСТНОГО РАСЧЕТА ОСНОВАНИЯ И КОНСТРУКЦИЙ СООРУЖЕНИЯ
Моделирование работы фундаментных плит - достаточно разработанная область геотехнических расчетов, в которой бесспорным является приоритет отечественных исследователей. Созданные еще в 1950 - 70-х годах модели упругого основания позволили с достаточной точностью учитывать пространственную работу грунта и выполнять совместные расчеты основания и плиты на существовавшем в то время уровне развития вычислительной техники. Среди этих моделей наиболее совершенными являлись модели Горбунова-Посадова и Пастернака.
Модель Горбунова-Посадова предполагает расчет с одним переменным коэффициентом постели, который определяется путем деления давления по подошве плиты на величину ожидаемой осадки в данной точке. Принцип расчета заключается в итерационном совмещении расчетов осадок упругого основания от давления по подошве плиты и расчетов усилий в плите от неравномерности осадок. Как показывает практика, недостаток такого подхода заключается в медленной сходимости итерационного процесса, что приводит к существенной трудоемкости и неэффективности расчетов. По этой причине данный принцип не получил распространения в расчетной практике и не был реализован в известных компьютерных программах.
|
Рис. 1. |
Существенно большее развитие на практике получили способы расчета с использованием постоянных коэффициентов постели. Как известно, модель с одним коэффициентом постели не позволяет учитывать пространственную работу грунта, взаимное влияние площадей нагружения и может привести к существенной недооценке усилий в плите. Эти недостатки были устранены Пастернаком, предложившим ввести второй коэффициент постели, учитывающий распределительную способность грунта. Им же были предложены формулы для вычисления коэффициентов постели для однослойного основания. |
Основным недостатком большинства упрощенных моделей, применяемых в расчетной практике, является то, что используемые в них параметры не удается получить из физико-механических характеристик грунтов основания. Кроме того, практически ни одна из моделей не позволяет оценить напряженно-деформированное состояние неоднородного массива грунта, а, следовательно, решение нелинейных задач с их помощью становится невозможным или весьма неточным.
- Рассмотрим обобщение двухпараметрической модели упругого основания, позволяющее избавиться от указанных недостатков.
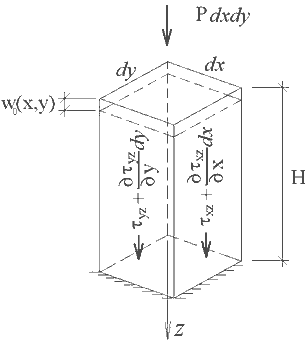
Выделим из массива грунта столбик размерами dx, dy и высотой H, нагруженный вертикальной нагрузкой P (рис 1). Предположим, что горизонтальные перемещения грунта малы по сравнению с вертикальными u(x,y,z)=v(x,y,z)=0. Обозначим
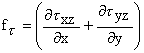 |
(1)
|
Рассматривая уравнения равновесия и формулы Коши можно получить уравнение,
содержащее неизвестную функцию![]() :
:
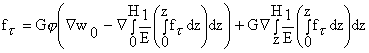 , , |
(2)
|
| где |
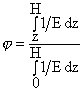 |
|
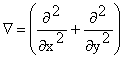 . . |
Модуль деформации грунта E0 и коэффициент Пуассона
![]() в общем случае
являются переменными по глубине. Представим функцию вертикального перемещения
поверхности грунтового массива w0(x,y) в окрестности точки (x,y)
многочленом 3-ей степени, таким, что
в общем случае
являются переменными по глубине. Представим функцию вертикального перемещения
поверхности грунтового массива w0(x,y) в окрестности точки (x,y)
многочленом 3-ей степени, таким, что
|
|
(3)
|
Тогда решением уравнения (2) будет функция
|
|
(4)
|
Подставив (4) в уравнение равновесия и формулы Коши после преобразований можно получить выражение вида
|
|
(5)
|
|
где
|
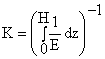 |
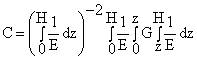 |
(6)
|
Вид выражения (5) аналогичен известному выражению для двухконстантной модели основания. При решении уравнения (2) использовалось приближенное представление функции w0, поэтому, используя выражение (6), мы будем получать приближенное решение задачи теории упругости при условии u(x,y,z)=v(x,y,z)=0. При постоянстве модуля деформации грунта по глубине можно получить известные выражения для коэффициентов жесткости двухконстантной модели основания, полученные ранее М.И.Горбуновым-Посадовым и П.Л.Пастернаком (Горбунов-Посадов М.И. Маликова Т.А. Расчет конструкций на упру-гом основании.; Пастернак П.Л. основы нового метода расчета фундаментов на упру-гом основании при помощи двух коэффициентов постели. - М.: гос-стройиздат, 1954. ). Для многослойного основания, состоящего из n слоев толщиной hi, можно получить следующие формулы:
|
|
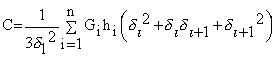 |
(7) |
|
где
|
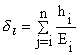 |
|
Формулы для коэффициентов жесткости многослойного основания, дающие близкие результаты, были получены И.А.Медниковым ( Медников И.А. Коэффициенты постели линейно-деформируемого многослойного основания// Основания фундаменты и механика грун-тов, 1967, №4.), однако в формуле для второго коэффициента жесткости им не была учтена переменность модуля сдвига по глубине.
Кроме уточнения формул для коэффициентов жесткости предложенный вывод параметров двухконстантной модели позволяет после вычисления функции перемещения поверхности вычислить значения всех компонентов напряжений в массиве грунта, а также перемещение w в любой точке массива:
![]()
![]()
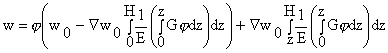
|
|
(8)
|
Зависимости (8) представляют собой "развертку" на полупространство решения задачи о перемещении поверхности грунтового массива по двухконстантной модели основания. Таким образом, решение задачи совместного расчета основания и сооружения по этой модели сводится к следующим этапам:
- 1. Определение параметров модели по данным о физико-механических характеристиках реального напластования грунтов основания, т.е. "свертка" пространственной задачи к задаче о перемещении точек на поверхности массива грунта.
2. Решение дифференциальных уравнений для точек, лежащих на поверхности грунтового массива и определение функции перемещений поверхности.
3. Определение напряженно-деформированного состояния основания по полученной функции перемещения поверхности (т.е. "развертка" решения).
- Далее с помощью известных методов (например, метода начальных напряжений) могут решаться нелинейные задачи механики грунтов.
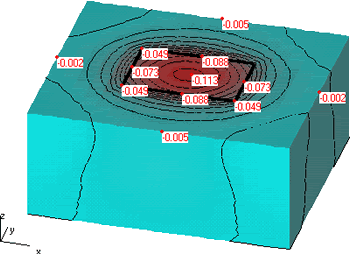
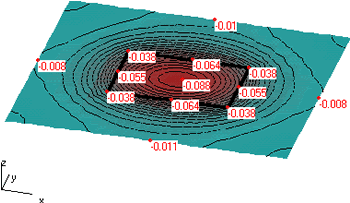
Как показывает проведенный нами анализ (Шашкин К.Г. Использование упрощенных моделей основания пдля решения задач совместного расчета основания и конструкций соору-жения// Реконструкция городов и геотехническое строительство 1999, №1.), расчеты по откорректированным формулам Медникова (7) и (8) дают удовлетворительное совпадение с расчетами по упругой пространственной модели грунта (рис. 2). Двухконстантная модель упругого основания была реализована во многих компьютерных программах, получивших широкое распространение.
 |
 |
| а) | б) |
Рис. 2. Сравнение расчета плиты по различным моделям основания. Изображены изолинии осадок (м): а) расчет плиты по пространственной упругой модели грунта; б) расчет плиты по двухконстантной модели.
Большой опыт проектирования фундаментных плит был накоплен крупнейшими петербургскими институтами - Ленпромстройпроектом, ЛенНИИпроектом. Специалисты этих институтов установили высокую планку компетентности в области таких расчетов для самых разнообразных по сложности сооружений. На западе расчеты такой степени сложности для рядовых сооружений применялись и применяются далеко не всегда, прежде всего (по признанию автора свода американских геотехнических норм (Bowles J.E. Foundation analysis and design. Fifth edition, 1996/)) из-за высокой стоимости собственно расчетов. В справедливости этого замечания нам пришлось убедиться и на практике, когда одна иностранная фирма безуспешно пыталась спроектировать для пивоваренного завода "Балтика" в С-Петербурге фундаментную плиту под цех с большими неравномерно распределенными нагрузками. Расчеты проводились ими по модели балки на упругом основании для условно вырезанной из плиты полосы шириной в 1 м, что привело к ошибкам в армировании плиты на 60% ее площади.
К сожалению, в последние годы в нашем городе наблюдается общее снижение уровня компетентности в области геотехнических расчетов, в том числе, и в расчетах фундаментных плит. Это связано, прежде всего, с появлением на рынке проектных услуг мелких фирм, не только не располагающих собственными специалистами-геотехниками, но и экономящих на расчетной части проекта. Практика работы одного из авторов в городской экспертной комиссии по основаниям и фундаментам показывает, что к расчетам зачастую привлекаются недостаточно подготовленные специалисты, незнакомые с основными предпосылками применяемых ими расчетных моделей. Наиболее распространенной ошибкой является неверное назначение коэффициентов в двухконстантной модели Пастернака. Злую службу здесь могут сослужить имеющиеся в справочниках таблицы коэффициентов постели, зависящих только от вида грунта. В то же время любому специалисту-геотехнику должно быть известно, что коэффициент постели включает в себя как физические, так и геометрические характеристики: глубину сжимаемой толщи, зависящую, в свою очередь, от размеров фундаментной плиты. Особенно много ошибок встречается при выборе второго коэффициента постели, который зачастую принимается произвольно, как якобы не влияющий на результаты расчета. Это заблуждение тесно связано с другой ошибкой - неучетом в расчетной схеме так называемых законтурных элементов. Существует мнение, что они также мало влияют на результаты расчета. Однако такой эффект наблюдается как раз при ошибочном назначении второго коэффициента постели (его занижении). Между тем, модель Пастернака была создана именно для учета пространственной работы грунта, в частности, за пределами нагруженной области.
Эти ошибки весьма опасны, поскольку приводят к принципиально неверной схеме работы плиты. Например, равномерно загруженная плита при подобных ошибках получает, согласно расчету, абсурдный для геотехника характер деформирования в виде выгиба с наибольшими осадками по краям загруженной области.
Оставив в стороне грубые ошибки, можно убедиться в том, что даже при корректном назначении параметров двухконстантной модели ее использование приводит к некоторым неточностям, связанным со слишком большой степенью упрощения работы массива грунта. Действительно, в большинстве случаев при выводе формул для коэффициентов постели пренебрегают горизонтальными деформациями в массиве грунта, что приводит к занижению расчетной осадки, которое в отдельных случаях может достигать 30%. Кроме того, при выводе формул для коэффициентов постели задаются приближенной функцией распределения напряжений по глубине грунтового массива (Власов В.З. Леонтьев Н.Н. Балки плиты и оболочки на упругом осно-вании. М. Госстройиздат, 1960.). Еще одним недостатком использования упрощенных моделей работы основания является невозможность учета нелинейной работы грунта. В целом для большинства моделей упругого основания характерным является преувеличение распределительной способности грунта, обусловливающее чрезмерное развитие мульды оседания. Это связано с допущениями, введенными при построении упрощенных моделей, а также отсутствием учета пластических деформаций, возникающих под краями плиты.
Методы расчета, в которых основание моделируется пространственными конечными элементами, лишены указанных недостатков. В этом случае работа грунта может быть описана различными нелинейными моделями, в наибольшей степени соответствующими рассматриваемой геотехнической ситуации, например, упругопластической моделью. Однако расчет совместного деформирования основания и плиты при моделировании основания пространственными конечными элементами оказывается достаточно сложной задачей. Действительно, для получения корректных значений усилий в плите требуется достаточно мелкая дискретизация расчетной схемы, что приводит к необходимости решать системы линейных алгебраических уравнений порядка 200000 неизвестных. До недавнего времени проводить подобные расчеты для рядовых сооружений было практически нереально, поскольку такая задача выдвигала слишком большие запросы к уровню ЭВМ и требовала огромных затрат машинного времени. Даже при современном уровне вычислительной техники большинство расчетных программ практически не справляется с подобными задачами, поскольку для их решения необходимо применение эффективных алгоритмов оперирования с большими системами линейных алгебраических уравнений.
| Ответы специалистов | Новости геотехники | Интернет-журнал |
| Семинары и конференции | Компьютерные программы | Полезные ссылки |