
![]()
N1, 1999
Использование упрощенных моделей основания для решения задач совместного расчета основания и конструкций сооружений
| Главная страница сайта |
| Титульная страница журнала |
| Содержание номера |
В настоящее время все большее применение находит численное моделирование работы конструкций сооружений. Разработано достаточно большое количество математических моделей, описывающих как конструкции надземной части здания, так и работу основания. Тем не менее приходится признать, что даже с учетом интенсивного развития вычислительной техники детальный совместный расчет основания и сооружения в обозримом будущем останется весьма затруднительной задачей. В связи с этим оказывается целесообразным поиск упрощений, существенно не сказывающихся на точности решения большинства задач.
Основным недостатком большинства упрощенных моделей, применяемых в расчетной практике, является то, что используемые в них параметры не удается получить из физико-механических характеристик грунтов основания. Кроме того, практически ни одна из моделей не позволяет оценить напряженно-деформированное состояние неоднородного массива грунта, а, следовательно, решение нелинейных задач с их помощью становится невозможным или весьма неточным.
Рассмотрим обобщение двухпараметрической модели упругого основания, позволяющее избавиться от указанных недостатков.
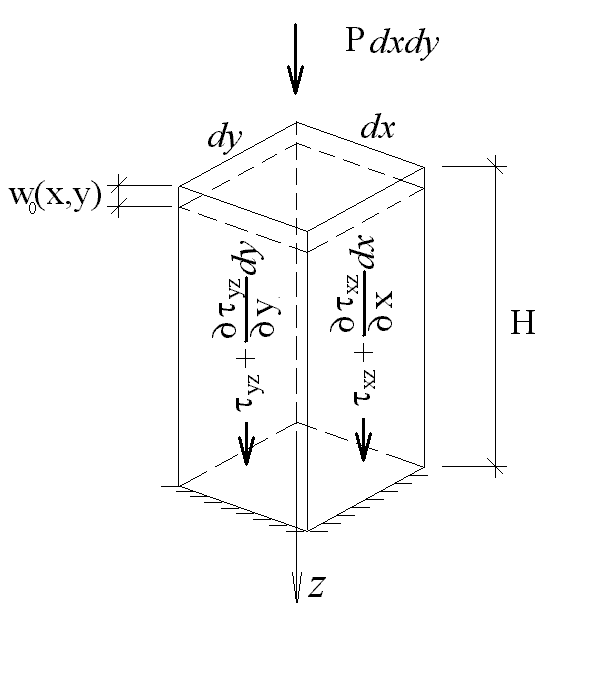
Рис. 1.
Выделим из массива грунта столбик размерами и высотой , нагруженный вертикальной нагрузкой (рис 1). Предположим, что горизонтальные перемещения грунта малы по сравнению с вертикальными
Обозначим
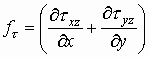 . (1)
. (1)
Рассматривая уравнения равновесия и формулы Коши можно получить уравнение,
содержащее неизвестную функцию ![]() :
:
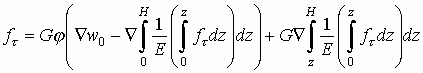 , (2)
, (2)
где
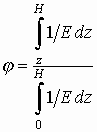 ,
, ![]() ,
,
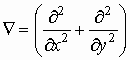 .
.
Модуль деформации грунта и коэффициент Пуассона ![]() в
общем случае являются переменными по глубине. Представим функцию вертикального
перемещения поверхности грунтового массива в окрестности точки многочленом
3-ей степени, таким, что
в
общем случае являются переменными по глубине. Представим функцию вертикального
перемещения поверхности грунтового массива в окрестности точки многочленом
3-ей степени, таким, что
![]() (3)
(3)
Тогда решением уравнения (2) будет функция
![]() . (4)
. (4)
Подставив (4) в уравнение равновесия и формулы Коши после преобразований можно получить выражение вида
![]() , (5)
, (5)
где
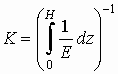 ,
, 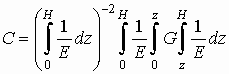 .
(6)
.
(6)
Вид выражения (5) аналогичен известному выражению для двухконстантной модели основания. При решении уравнения (2) использовалось приближенное представление функции , поэтому, используя выражение (6), мы будем получать При постоянстве модуля деформации грунта по глубине можно получить известные выражения для коэффициентов жесткости двухконстантной модели основания, полученные ранее М.И.Горбуновым-Посадовым и П.Л.Пастернаком [1,2]. Для многослойного основания, состоящего из слоев толщиной , можно получить следующие формулы:
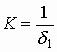 ,
,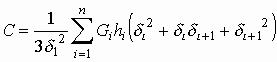 ,
(7)
,
(7)
где
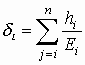 ,
, ![]() .
.
Формулы для коэффициентов жесткости многослойного основания, дающие близкие результаты, были получены И.А.Медниковым [3], однако в формуле для второго коэффициента жесткости им не была учтена переменность модуля сдвига по глубине.
Кроме уточнения формул для коэффициентов жесткости предложенный вывод параметров двухконстантной модели позволяет после вычисления функции перемещения поверхности вычислить значения всех компонентов напряжений в массиве грунта, а также перемещение в любой точке массива:
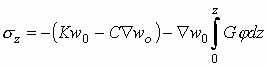 ;
;
![]() ;
;
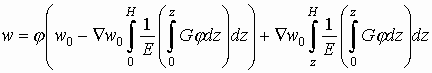 ;
;
![]() . (8)
. (8)
Зависимости (8) представляют собой “развертку” на полупространство решения задачи о перемещении поверхности грунтового массива по двухконстантной модели основания. Таким образом, решение задачи совместного расчета основания и сооружения по этой модели сводится к следующим этапам:
1. Определение параметров модели по данным о физико-механических характеристиках реального напластования грунтов основания, т.е. “свертка” пространственной задачи к задаче о перемещении точек на поверхности массива грунта.
2. Решение дифференциальных уравнений для точек, лежащих на поверхности грунтового массива и определение функции перемещений поверхности.
3. Определение напряженно-деформированного состояния основания по полученной функции перемещения поверхности (т.е. “развертка” решения).
Далее с помощью известных методов (например, метода начальных напряжений) могут решаться нелинейные задачи механики грунтов.
Как показывает практика, решения с использованием формул (7) и (8) дают вполне приемлемое для реальных расчетов совпадение результатов с решениями по теории упругости для плитных и ленточных фундаментов. При этом сложность решения (определяющаяся порядком и степенью заполненности матрицы разрешающей системы линейных уравнений) может быть снижена в десятки и сотни раз. Это дает возможность эффективно производить расчеты с учетом совместной работы конструкций зданий и основания. Рассмотрим пример такого расчета.
Рассматриваемое здание, расположенное в Санкт-Петербурге по адресу Очаковская ул. д. 5, было построено на рубеже XIX-XX веков. В 1950-х годах к нему был пристроен дом 3, в результате чего дом 5 получил неравномерные осадки. Полученный по расчету характер осадок (рис. 2) хорошо согласуется с наблюдаемым в действительности. В 1999 году было закончено строительство примыкающего с другой стороны дома 7.
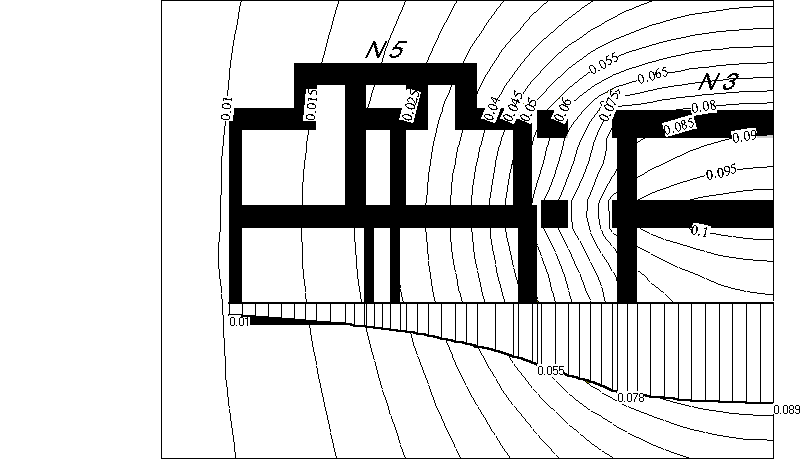
Рис. 2. Эпюры и изолинии (м) осадок дома 5 от возведения дома 3.
Как показали расчеты и геодезические наблюдения, принятая в проекте дома 7 схема консольного примыкания нового здания с размером консоли 1.2 м не могла обеспечить сохранность дома 5. Развивающиеся в настоящее время неравномерные осадки дома 5 уже привели к образованию трещин в кладке стен. Согласно расчету прогнозируемая величина осадок дома 5 достигает 10 см. При этом дом получает деформацию выгиба со стрелой 19 мм, что в сумме с уже имеющимся выгибом от строительства дома 3 может привести к разрушению здания.
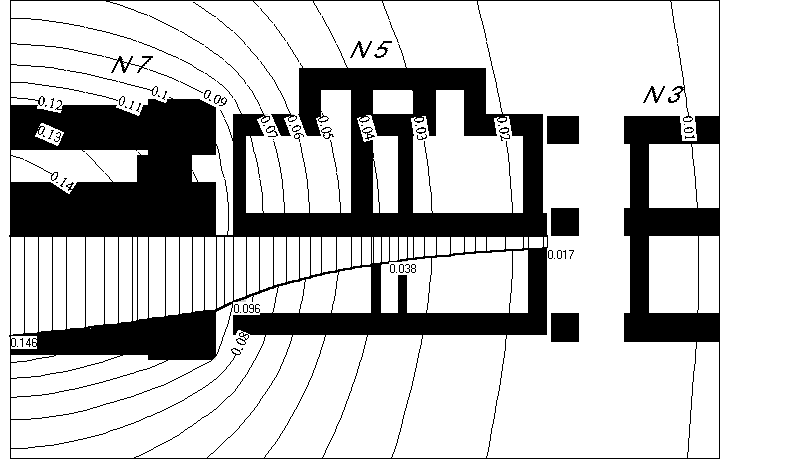
Рис.3. Эпюры и изолинии (м) осадок дома 5 от возведения дома 7.
В связи с этим были рассмотрены возможные варианты усиления дома 5. Вариант пересадки здания на свайные фундаменты в данном случае оказался трудновыполнимым по технологическим и экономическим соображениям. Поэтому был выбран вариант повышения пространственной жесткости здания путем устройства в пределах подвальных помещений жесткой коробчатой конструкции. Расчеты показывают (рис.4), что предлагаемое усиление существенным образом перераспределяет осадки здания, приближая эпюру осадок практически к треугольной, характерной для осадок жесткого штампа. Таким образом, устраняется причина, приводящая к раскрытию трещин, и здание получает крен как жесткое целое без деформаций надземных конструкций.
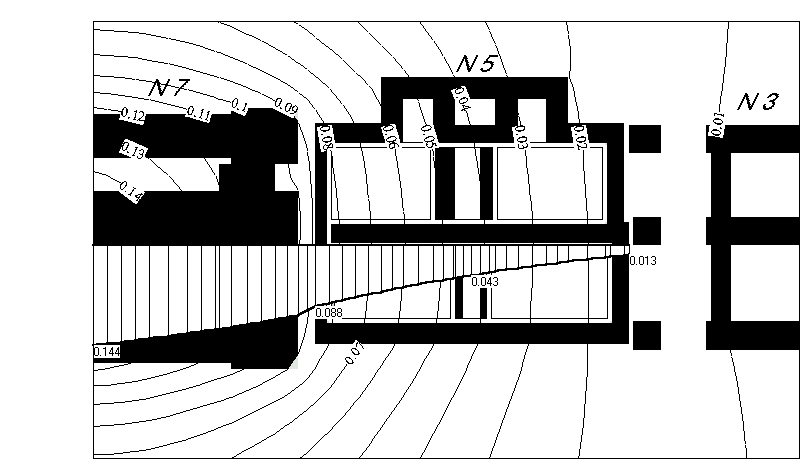
Рис.4. Эпюры и изолинии (м) осадок дома 5 от возведения дома 7 с учетом усиления.
Приведенный расчет был выполнен с помощью разработанной авторами программы, реализующей методом конечных элементов расчет плитных и балочных конструкций, а также позволяющей учитывать пространственную работу грунта, описанного в соответствии с изложенной выше моделью. Параметры двухконстантной модели вычислялись по данным о механических характеристиках грунтов основания. Полученные значения осадок практически совпадают с осадками, полученными при расчете различных сечений в плоской постановке (такие расчеты производились с помощью программы “Геомеханика”, разработанной под руководством проф. А.Б.Фадеева, которая реализует методом конечных элементов решение плоских упругопластических задач). Такое совпадение подтверждает корректность использования описанной двухконстантной модели. При моделировании пространственной работы грунта по двухконстантной модели решалась система из 12276 линейных уравнений. Для решения подобной задачи с использованием пространственных конечных элементов, моделирующих массив грунта, потребовалось бы решить систему из примерно 400000 линейных уравнений, что в настоящее время трудноосуществимо.
Таким образом, приведенный пример показывает эффективность использования рассмотренной модели для анализа геотехнических ситуаций, прогноза дальнейшего развития осадок, а также для выбора оптимального варианта усиления и расчета конструкций усиления.
Литература
1. М.И.Горбунов-Посадов. Расчет конструкций на упругом основании. Госстройиздат. 1953.
2. П.Л.Пастернак. Основы нового метода расчета фундаментов на упругом основании при помощи двух коэффициентов постели. Госстройиздат. 1954.
3. Медников И.А. Коэффициенты постели линейнодеформируемого многослойного основания //Основания фундаменты и механика грунтов, 1967, №4.
| Ответы специалистов | Новости геотехники | Интернет-журнал |
| Семинары и конференции | Компьютерные программы | Полезные ссылки |